CFA® Fixed Income
Summary, Syllabus, Topics, and Sample Questions (L1, L2, L3)

The CFA Institute Fixed Income curriculum delves into the vast and critical realm of fixed income securities, commonly referred to as bonds. These financial instruments serve as the cornerstone for raising capital across the globe, facilitating the financial needs of institutions, governments, and various other entities.

Fixed income instruments offer a broad spectrum of utility, serving both investors and issuers with purposes ranging from income generation and safeguarding of principal to intricate asset-liability management. Notably, the assessment of credit risk associated with fixed-income securities has gained profound significance since the aftermath of the global financial crisis in 2008.

The Fixed Income segment of the curriculum is renowned for its quantitative nature, and it ranks among the more challenging areas covered in the CFA exam. Its prominence is sustained throughout all three levels, making it a pivotal component of the CFA program. Within this subject matter, candidates are introduced to an extensive array of financial concepts and formulas that are indispensable for proficient financial analysis, whether within the purview of fixed income or in broader financial contexts.

Level 1

Level 2

Level 3

Level 1

What to Expect in CFA Level 1 Fixed Income?

On the CFA Institute’s Level 1 exam, Fixed Income is among the top three most heavily weighted topics, along with Financial Statement Analysis and Ethics.

Candidates are taught to define fixed income securities and calculate and interpret their associated features. The material covers securitization, the fundamentals of credit risk, and the influence of interest rates on bond returns.

Exam Weighting

The CFA Fixed Income topic has a weight of 11-14% of the total exam content, so that approximately 20-25 of the 180 CFA Level 1 exam questions focus on this topic.

Topic Weight	No. of Learning Modules	No. of Formulas	No. of Questions
11-14%	19	ca. 40	20-25

Level 1 Fixed Income 2024 Syllabus, Readings, and Changes

The CFA Level 1 curriculum has about 19 readings for Fixed Income (8.2% of the total curriculum).

No. of Learning Modules – 19	No. of LOS – 51
Summary The learning modules introduce attributes of various Fixed Income securities and how to calculate and interpret bond prices, yields, and spreads, and then also introduces securitization and provides an overview of global debt markets. The material covers fundamentals of bond returns and risks with special attention given to interest rates and credit risk. It also introduces key factors for assessing bond sensitivity and credit analysis.

Fixed-Income Instrument Features

The focus of the topic is on understanding fixed-income instruments, encompassing the description of their features. Additionally, candidates are expected to delve into the contents of a bond indenture, emphasizing the ability to contrast affirmative and negative covenants.

Fixed Income Markets: Issuance, and Trading

Global Fixed Income markets include both publicly traded securities and non-publicly traded loans. These markets typically attract less attention despite being three times larger than global equity markets.

The learning module presents a summary of global fixed income markets and their major players.
Candidates will be introduced to fixed income indexes and fixed income trading in secondary markets.

Fixed-Income Cash Flows and Types

this topic focuses on comprehending fixed-income cash flows and types. This involves describing the common cash flow structures of fixed-income instruments and contrasting cash flow contingency provisions that benefit both issuers and investors. Additionally, candidates are expected to articulate how legal, regulatory, and tax considerations impact the issuance and trading of fixed-income securities.

Fixed-Income Markets for Corporate Issuers

Many kinds of assets generate cash flows for their investors, such as mortgages, auto loans, student loans, bank loans, etc. When those cash flows are securitized, they pass through an entity that repackages them as fixed income securities, and their cash flows become the basis of that asset’s value. Special entities issue these securities as asset-backed securities (ABS).

Candidates will be introduced to the benefits of securitization for investors, issuers, economies, and financial markets.
The learning module also explores the various characteristics of different ABS types and their associated risks.

Fixed-Income Markets for Government Issuers

The focus of this topic is on understanding funding choices made by sovereign and non-sovereign governments, quasi-government entities, and supranational agencies. Candidates are expected to describe these funding choices. Furthermore, the topic involves contrasting the issuance and trading of government and corporate fixed-income instruments.

Yield and Yield Spread Measures: Fixed Rate Bonds and Floating Rate Instruments

The focus of this section is on the ability to calculate the annual yield on a bond for varying compounding periods within a year. Additionally, candidates are expected to compare, calculate, and interpret yield and yield spread measures for fixed-rate bonds. Similarly, in the context of yield and yield spread measures for floating-rate instruments, the emphasis is on the capability to calculate and interpret yield spread measures for such instruments and calculate and interpret yield measures specifically tailored for money market instruments.

Fixed-Income Risk and Credit Analysis (An Overview)

This section covers essential concepts in fixed-income risk and credit analysis:

Yield-Based Bond Measures	Define and interpret modified duration, money duration, and PVBP. Explore the impact of maturity, coupon, and yield on a bond’s interest rate risk.
Yield-Based Bond Convexity and Portfolio	Calculate and interpret convexity and its adjustment. Assess bond price change for a yield shift, considering duration and convexity. Calculate portfolio duration and convexity, acknowledging their limitations.
Curve-Based and Empirical Risk Measures	Understand effective duration and convexity for bonds with embedded options. Calculate bond price change for benchmark yield shifts using these measures. Define key rate duration and distinguish empirical from analytical duration.
Credit Risk	Define credit risk components and analyze factors influencing yield spread levels. Evaluate the uses and limitations of credit ratings from agencies.
Credit Analysis for Government and Corporate Issuers	Considerations for sovereign and non-sovereign government debt evaluation. Quantitative and qualitative factors in corporate credit analysis. Interpret financial ratios and understand debt seniority rankings.
Fixed-Income Securitization	Outline securitization benefits for issuers, investors, and markets. Describe the securitization process and the roles played by involved parties.

CFA Fixed Income Level 1 Sample Questions and Answers

The sample questions are typical of the probing multiple-choice questions on the CFA L1 exam. During the exam, you have about 90 seconds to read and answer each question, carefully designed to test knowledge from the CFA Curriculum. UWorld’s question bank is built to expose you to exam-like questions and illustrate and explain the concepts tested thoroughly.

Question 1
Question 2
Question 3

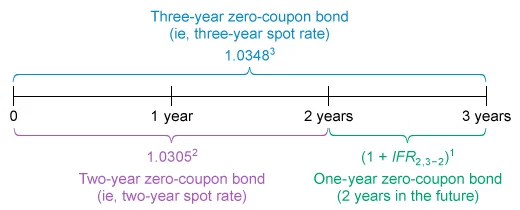
An analyst has gathered the following information on zero-coupon government bond yields:

Maturity	Spot Rate
1 year	2.42%
2 years	3.05%
3 years	3.48%
4 years	3.65%

If the rates are based on a periodicity of 1, the one-year forward rate 2 years in the future (2y1y) is closest to:

3.72%
4.16%
4.35%

Submit

A two-year floating-rate note pays three-month Libor plus 15 basis points. The floater is priced at 99.60 per 100 par value, three-month Libor is currently 1.45%, and the coupon reset today. Assuming a 30/360 day-count convention and quarterly coupon payments, the discount margin in basis points (bps) is closest to:

35 bps
40 bps
45 bps

Submit

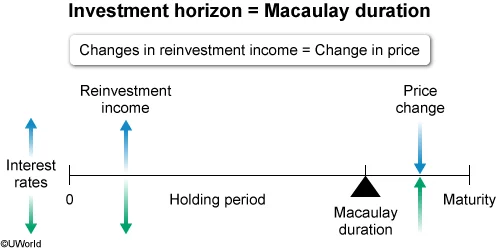
A coupon bond’s Macaulay duration is most accurately described as the holding period over which:

the value of cash flows received equal the cost of buying the bond.
changes in reinvestment income offset changes in the bond’s price.
the bond earns a risk-free return if hedged by shorting a government bond.

Submit

Level 2

What to Expect in CFA Level 2 Fixed Income?

The CFA Level 2 Fixed Income is one of the most heavily weighted topics on the exam. The material introduces traditional and modern theories regarding the shape of the yield curve and the fundamental relationships underpinning its composition. Candidates will study valuation methods used to value bonds with embedded options and various credit analysis concepts.

Exam Weight

The CFA Fixed Income topic has a weight of 10-15% of the total exam content, so that approximately 8-12 questions or 2-3 item sets on the CFA Level 2 exam focus on this topic.

Topic Weight	No. of Readings	No. of Formulas	No. of Questions
10-15%	5	ca. 60	ca. 11

Level 2 Fixed Income Syllabus, Readings, and Changes

The CFA Level 2 curriculum includes 5 total learning modules for 2024, for the Fixed Income topic (10% of the total curriculum). There have been no changes to the L2 Fixed Income curriculum in 2024, except for minor updates.

No. of Learning Modules – 5	No. of LOS – 50
Summary The Fixed Income curriculum introduces the yield curve and fundamental aspects of its composition. Candidates will learn various theories regarding yield curve shape and an arbitrage-free framework for valuing option-free bonds. It then builds on binomial valuation methods to value bonds with embedded options. Candidates will study credit analysis, the term structure of credit spreads, and how credit default swaps are used in managing credit exposure.

The Term Structure and Interest Rate Dynamics

Interest rates act to both influence and measure the economy. Quantifying interest rate risk is an important skill for risk managers, and understanding the determinants of interest rates is important for issuers of and investors in fixed income securities.

The learning module explains spot rates and forward rates and their influence on the yield curve shape.
Candidates will build on this information to understand how forward rates influence the yield-to-maturity and expected bond returns.

The Arbitrage-Free Valuation Framework

Valuing fixed income securities, derivatives, and other financial assets is predicated on the idea that market prices adjust until arbitrage opportunities expire.

The learning module introduces concepts and techniques for no-arbitrage valuation of Fixed Income securities.
This includes discussions of the binomial interest rate tree and a Monte Carlo forward-rate simulation.

Valuation and Analysis of Bonds with Embedded Options

The value of embedded options is typically contingent on interest rates. This makes bond valuation more complex when a bond has one or more embedded options. Bond issuers and investors must understand how various embedded options influence bond values and their sensitivity to interest rate changes.

The learning module introduces a summary of different types of embedded options before exploring bonds that include a call or put provision.
Candidates will also learn about how option-adjusted spreads are used to value risky callable and putable bonds.

Credit Analysis Models

Credit analysis models rely on inputs such as exposure to default loss, the loss given default, and the probability of default. These models are an important part of valuing corporate and government bonds.

Candidates are introduced to structural and reduced-form credit analysis models.
The learning module also covers the arbitrage-free framework and compares the credit analysis for securitized debt with that of corporate bonds.

Credit Default Swaps

A credit default swap is a financial contract between two parties that enables an investor to “swap” or offset credit risk with another investor for a defined period of time. These derivative instruments are broadly used internationally.

The learning module classifies these instruments and explores the fundamental concepts behind them.
Candidates will learn about the elements associated with their valuation, pricing, and applications.

CFA Fixed Income Level 2 Sample Questions and Answers

The sample questions here are typical of the L2 exam’s complexity and depth: formatted as item sets, with a vignette to deliver a scenario that tests the CFA L2 Curriculum. (On the actual exam, each vignette applies to four questions; we’ve thrown in a couple extra to get a bit more learning in). And be sure to review the illustrated explanations we’ve provided for each question: UWorld’s question bank is designed to expose you to exam-like questions and explain the concepts tested thoroughly.

Question 1
Question 2
Question 3

Which of the three approaches for the arbitrage-free valuation of option-free bonds described by Muon is least likely correct?

Approach 1
Approach 2
Approach 3

Submit

Explanation

Approach 1: Value the bond as a portfolio of zero-coupon bonds that replicate the bond’s cash flows.

Approach 2: Value the bond as the sum of the individual cash flows’ present values, discounting each cash flow by the spot rate with a matching term.

Approach 3: Value the bond as the sum of the individual cash flows’ present values, discounting each cash flow by the YTM of a benchmark bond with the same time to maturity as the bond.

Arbitrage-free valuation of option-free bonds is based on the no-arbitrage principle: market prices adjust until there is no possibility of making risk-free profits through the simultaneous purchase and sale of related assets. This principle is based on two related, fundamental concepts.

The law of one price: Assets that are perfect substitutes (eg, same asset traded in different markets, an asset and its related forward contract) must trade at equivalent values.
Value additivity: The value of the whole must equal the sum of the value of its parts.

The arbitrage-free pricing of a coupon bond reflects these concepts by discounting individual cash flows by the spot rate with a term that matches the bond’s payment dates (Choice B). This approach values the bond as a portfolio of zero-coupon bonds that replicate the amount and timing of the bond’s coupons and principal (Choice A). As a result, each discount rate incorporates any risks captured in market term premiums.

Discounting a coupon bond’s cash flows by a single rate (as suggested in Approach 3) is inappropriate for estimating the bond’s arbitrage-free value—unless the yield curve is flat, which is clearly not the case in this instance (Exhibits 1 and 2). If the single discount rate were the bond’s YTM, the result would be the bond’s market price, which could never reveal an arbitrage opportunity. In addition, a single rate would not reflect any difference in risk (eg, expected inflation) from the variation of interest rates across maturities.

Things to remember:
The arbitrage-free valuation of option-free bonds is based on value additivity and the law of one price. These two concepts are applied to a coupon bond by discounting the bond’s individual cash flows by the appropriate-term spot rate. This treats the bond as a portfolio of zero-coupon bonds that match the amount and timing of the bond’s coupons and principal.

Based on Exhibits 1 and 2, which bond has a market price that best reflects its arbitrage-free price?

Bond A
Bond B
Bond C

Submit

Explanation

Exhibit 1 US Benchmark Par Curve Bonds
Maturity (years)	YTM
1	1.50%
2	2.00%
3	2.50%

Exhibit 2 Summary Data for US 3-Year Bonds
	Coupon rate	Market price
Bond A	2.50%	100.251
Bond B	3.00%	101.737
Bond C	3.50%	102.847

Arbitrage-free 3-year coupon bond price

P₀ =

PMT / [ 1 + r ( 1 ) ]¹

PMT / [ 1 + r ( 2 ) ]²

PMT + 100 / [ 1 + r ( 3 ) ]³

P₀ = Arbitrage-free price
PMT = Periodic coupon
r ( J ) = J – period spot rate

The arbitrage-free value of a coupon bond is the sum of the present value of the bond’s cash flows discounted by the appropriate-term spot rates. Violations of the no-arbitrage principle are uncovered by comparing a bond’s arbitrage-free value, based on a spot rate curve, to the bond’s market price, based on a single discount rate (ie, the bond’s YTM).

Bootstrapping a spot rate from a par bond

1 =

PBC_N / [ 1 + r ( 1 ) ]¹

+ … +

PBC_N + 1 / [ 1 + r ( N ) ]^N

PBC_N = Par bond coupon for bond with N years to maturity
r ( J ) = J – period spot rate
N = Number of periods to maturity

Spot rates are bootstrapped from a benchmark (eg, government bond) par yield curve. Bootstrapping is an iterative process that extends a spot rate curve one period at a time. Each iteration uses a par bond with a maturity equal to the term of the spot rate being calculated.

A par bond has a price of 1.00 (ie, 100% of par) and a coupon rate equal to its YTM. Each cash flow before maturity is discounted by the (previously calculated) appropriate-term spot rate. The cash flows are known, as are all spot rates except the one for the final period. Using the bootstrapping equation from above, solve for the final-period discount rate, which is the spot rate for a term matching the bond’s maturity.

The 1-year spot rate is equal to the 1-year par rate: 1.50%.

The 2-year spot rate is calculated by rearranging the equation as follows:

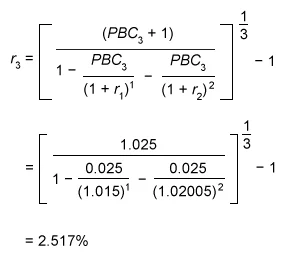
The 3-year spot rate is calculated as follows:

Use the spot rates bootstrapped from the par bond rates to calculate the arbitrage-free values of the bonds. However, note that Bond A requires no calculation: since the bond has a coupon rate equal to the 3-year par bond YTM, it has an arbitrage-free value equal to 100% of par.

	Arbitrage-free value	Market price
Bond A	2.5 / (1.015)¹ + 2.5 / (1.02005) ² + 102.5 / (1.02517) ³ = 100.000	100.251
Bond B	3.0 / (1.015)¹ + 3.0 / (1.02005) ² + 103.0 / (1.02517) ³ = 101.437	101.737
Bond C	3.5 / (1.015)¹ + 3.5 / (1.02005) ² + 103.5 / (1.02517) ³ = 102.874	102.847

Things to remember:
The arbitrage-free value of a coupon bond is the sum of the present value of the bond’s cash flows discounted by the appropriate-term spot rates. The spot rates for an arbitrage-free valuation can be bootstrapped from a par bond curve.

Based on Exhibit 3, if Muon assumes a volatility of 20%, the interest rate at the higher-rate node at Time 1 is closest to:

1.40%
1.72%
3.13%

Submit

Explanation

Binomial interest rate trees are based on a benchmark yield curve. For all periods beyond Time 0, the tree consists of 1-period forward rates, which are calculated through a trial-and-error process using:

a benchmark bond maturing one period beyond the previously obtained rates,
an assumed volatility that is the same for the entire tree,
the benchmark yield curve 1-period spot rate, and
1-period forward rates obtained from all previous iterations of this process.

Binomial rate tree construction requires assumptions about how interest rates change. The standard approach is to assume interest rate changes are lognormally distributed. This assumption leads to the relationship between the rates at adjacent nodes at a given period of time, as shown in this tree. To calculate the 1-period higher forward rate, use the 1-period lower forward rate (i_1,L) and the given volatility (20%).

i_1,H	= i_1,L× e²^σ
	= 0.0115 × e^2(0.2)
	= 0.0115 × 1.492
	= 1.72%

Note: The “lower” rate one period in the future is not necessarily below the interest rate at the previous node; it is lower relative to the “higher” rate for that period. Depending on the slope of the benchmark spot rate curve, the “lower” rate at the next period could be either above or below the interest rate at the preceding node.

(Choice A) 1.40% results from multiplying i_1,L by e², which fails to reflect that the exponent is 2 times the volatility.

(Choice C) 3.13% results from multiplying i_1,L by e, which is incorrect since e must be raised to the power of 2 times the volatility.

Things to remember:
Rates on a binomial interest rate tree are calculated through a trial-and-error process, using benchmark bonds and an assumed volatility. For two adjacent nodes at a given time period, the higher rate is derived from the lower interest rate and the assumed volatility.

Level 3

What to Expect in CFA Level 3 Fixed Income?

The CFA Level 3 Fixed Income topic is the second most heavily weighted topic on the exam, with a weight of 15-20%.
The two study sessions discuss the role played by fixed income securities in portfolios and introduce fixed income
mandates before revisiting the yield curve and its association with fixed income portfolios.

Exam Weighting

The CFA Fixed Income Portfolio Management topic has a weight of 15-20% of the total exam content,
meaning that approximately 24-30 questions or 3-4 items sets and essay vignettes on the CFA Level 3 multiple choice exam questions focus on
this topic.

Level 3 Fixed Income Syllabus, Readings, and Changes

The CFA Level 3 curriculum for 2024 comprises four readings, reflecting an
increase of two readings compared to the 2023 curriculum.

No. of Readings	No. of LOS
4	33
Summary Discusses the role of fixed income securities in portfolios and introduces liability-based and total return mandates. Candidates will learn about fixed income portfolio risk measures and alternatives to direct bond investments. The session concludes with liability-driven and index-based strategies.

Overview of Fixed Income Portfolio Management

Fixed income instruments run the gamut from publicly traded securities to non-publicly traded instruments. Investors
use these instruments to generate regular income from their investments until their capital is returned at a
predetermined date.

The reading discussed the various roles of fixed income securities in portfolios, fixed income mandates, and
bond market liquidity.
Candidates will also cover portfolio measures, instruments, and vehicles used in fixed income portfolio
management.

Liability-Driven and Index-Based Strategies

Passive fixed income investment strategies go beyond buy-and-hold strategies. Bond portfolios can be
routinely rebalanced using strategies like immunization and indexation. The reading covers such strategies alongside
strategies for liability-driven investing.

Candidates will learn how to develop and structure fixed income portfolios with assets and liabilities in mind.

Yield Curve Strategies

Active fixed income management involves deviating from the primary risk factors associated with an index. To generate
excess returns, analysts must assess the yield curve and develop a portfolio with interest rates in mind.

The reading primarily covers fixed income yield curve management strategies to exceed the returns of a benchmark
index due to yield curve changes.

Fixed Income Active Management: Credit Strategies

The reading emphasizes credit spreads and how to quantify the effect of spread changes on portfolio value. Candidates
will review other expected fixed income return components and learn about credit spread measures for fixed- and
floating-rate bonds.

Study Tips for CFA Fixed Income

If you are a fixed income professional, this section might come more easily for you, but don’t even think about skipping it. Fixed income is critical for every level of the CFA exams.
On the other hand, if you are like most CFA candidates and are not a fixed income professional, this will be some of the least familiar, most quantitative, and most difficult material in the curriculum. The silver lining is that it is all quite logical and methodical. Plan to put in the time to thoroughly go over the Fixed Income readings.
Level 3 is all about portfolio management, and fixed income instruments are critical to any well-diversified portfolio. The vast bulk of the problems at this level are theoretical. But, you'll also need to do some math.
The best advice for both Level 2 and Level 3 is to review and refresh the material from the previous levels.

Visit our CFA Level 1 Study Guide and CFA Level 2 Study Schedule for more information.

Frequently Asked Questions

Is CFA Level 1 Fixed Income Hard?

CFA Level 1 Fixed Income is considered one of the more difficult topics on the exam, and for most candidates, it is also one of the least familiar. Fixed income securities are typically more abstract than equity investments. Furthermore, candidates are often more familiar with the stock exchange and equity investments than they are with debt securities.

The earning modules are highly theoretical and laden with novel terms. Candidates are introduced to several methods of bond valuation and complicated concepts related to risk and return analysis. However, having a solid understanding of Fixed Income is critical to the CFA charter.

Is the CFA Level 2 Fixed Income topic hard?

Like its Level 1 counterpart, the CFA Level 2 Fixed Income is considered one of the more difficult topics on the exam. Fixed income is relatively heavy on both formulas and theory. Candidates will study various formulae used to value bonds with embedded options and the theoretical and practical aspects of the yield curve.

How Can I Study Level 3 Fixed Income for the CFA exam?

To get the best of both worlds, think about combining the CFA curriculum with a third-party prep provider, like UWorld. The End of Chapter (EOC) questions from the CFA Institute are comprehensive, and third-party study resources are condensed and time-efficient.

For constructed response sessions, you need to practice a lot, ideally in an exam setting. Improve your ability to self-grade essay questions and become a master at responding to them. If you are running short on time, go over the questions and sample answers to complete your review prior to the test. Don’t overlook or undervalue the item set session. This is most likely going to increase your overall score.

CFA® Fixed Income
Summary, Syllabus, Topics, and Sample Questions (L1, L2, L3)

What to Expect in CFA Level 1 Fixed Income?