| Derivative Investments | ||
|---|---|---|
| Topic Weight | Number of Questions | |
| Level 1 | 5-10% | 4-8 |
| Level 2 | 5-8% | 9-14 |
Forward commitments entail a contractual obligation between parties to execute a predetermined transaction at a future date, with terms agreed upon in advance. In contrast, contingent claims grant a party the right, but not the obligation, to partake in a prospective transaction under specified conditions.
Derivative investments are traded through 2 primary channels: exchange-traded and over-the-counter (OTC). Exchange-traded derivatives adhere to standardized terms and conditions, whereas OTC-based derivatives offer greater customization options to investors.
The most common Derivative Investments used by investors are:
- Future Contracts
- Options (call and put)
- Forward Contracts
- Swaps
- Credit Default Swaps
What to Expect in CFA® Level 1 Derivative Investments
The Derivative Investments curriculum has a similar weighting to that of alternative investments and portfolio management. There are 10 Level 1 learning modules dedicated to the topic. You will study various derivative instruments classified as forward commitments and contingent claims and see how they derive their value and are traded in different settings.
Exam Weighting
The CFA Level 1 Derivative Investments has a weighting of 5-8% which implies that around 9-14 out of 180 CFA Level 1 exam questions focus on this topic.
| No. of Learning Modules | No. of Formulas |
|---|---|
| 10 | Around 12 |
Level 1 Derivative Investments 2026 Syllabus, Readings, & Changes
There are 10 learning modules for CFA Level I DI in 2026. These learning modules begin with an overview of derivative instruments and markets, distinguishing characteristics of forward commitments and contingent claims, and the derivative’s relation to the underlying asset. They then cover the purpose, benefits, and risks of Derivative Investments, as well as criticisms and potential misuse.
The material remains essentially unchanged, with minor updates. The following table provides a brief description of the topic curriculum:
| No. of Learning Modules – 11 | No. of LOS – 22 | |
|---|---|---|
Summary This paper discusses the fundamentals of derivative instruments, including forward commitments (e.g., futures, forwards, swaps) and contingent claims (e.g., call and put options), and derivative markets such as exchange-traded and over-the-counter derivative markets. It further explains derivative pricing and valuation and introduces the principle of arbitrage. | ||
Derivative Instrument and Derivative Market Features
The reading focuses on defining derivatives and elucidates the basic features of derivative instruments. It also provides insights into the characteristics of derivative markets, distinguishing between over-the-counter and exchange-traded markets.
Forward Commitment and Contingent Claim Features and Instruments
This reading emphasizes defining various derivative instruments such as forward contracts, futures contracts, swaps, options (calls and puts), and credit derivatives. It also involves comparing their essential characteristics and understanding the value and profit determination for call-and-put options.
Derivative Benefits, Risks, and Issuer and Investor Uses
The focus here is on describing the benefits and risks associated with derivative instruments. Additionally, it compares how derivatives are utilized among issuers and investors.
Arbitrage, Replication, and the Cost of Carry in Pricing Derivatives
This reading centers on explaining the concepts of arbitrage and replication in pricing derivatives. It also differentiates between the spot and expected future prices of an underlying asset and the cost of carry associated with holding the underlying.
Pricing and Valuation of Forward Contracts and for an Underlying with Varying Maturities
The primary focus of this reading is to explain the determination of the value and price of a forward contract throughout its life. It also covers the determination of forward rates for interest rate forward contracts and their applications.
Pricing and Valuation of Futures Contracts
Here, the reading aims to compare the value and price of forward and futures contracts while explaining the reasons for the differences in forward and futures prices.
Pricing and Valuation of Interest Rates and Other Swaps
This reading delves into how swap contracts are similar to, yet different from, a series of forward contracts. It also contrasts the value and price of swaps.
Pricing and Valuation of Options
This reading’s primary focus is to explain an option’s exercise value, moneyness, and time value. It also contrasts the use of arbitrage and replication concepts in pricing forward commitments and contingent claims, identifying factors influencing option value.
Option Replication Using Put–Call Parity
In this reading, the emphasis is on explaining put–call parity for European options and put-call-forward parity for European options.
Valuing a Derivative Using a One-Period Binomial Model
This reading revolves around explaining how to value a derivative using a 1-period binomial model and describing the concept of risk neutrality in derivatives pricing.
CFA Derivative Investments Level 1 Sample Questions and Answers
These sample questions are typical of the probing multiple-choice questions on the L1 exam. During the exam, you have about 90 seconds to read and answer each question, carefully designed to test knowledge from the CFA curriculum. UWorld’s question bank is built to expose you to exam-like questions and illustrate and explain the concepts tested thoroughly.
An analyst observes the following market data for one American put option:
| Selected Data | |
|---|---|
| (in CAD) | |
| Stock price | 48 |
| Strike price | 50 |
| Option premium | 4 |
This option’s moneyness is best described as:
- in the money.
- at the money.
- out of the money.
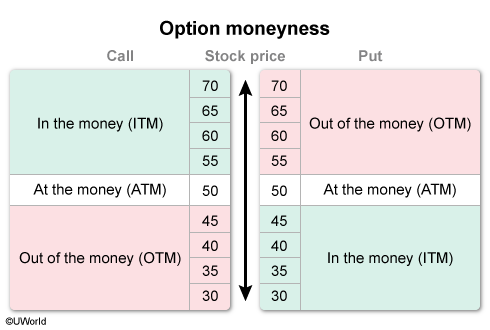
Moneyness refers to the relationship between an option’s strike price and the underlying stock price and is indicative of the option’s intrinsic value. An option trading at the money or out of the money has no intrinsic value. An option trading in the money has intrinsic value:
- For an in-the-money call option, the underlying stock price is greater than the strike price. This gives the call owner the right to buy the stock at a price lower than the market price, which in turn gives the option intrinsic value.
- For an in-the-money put option, the strike price is greater than the underlying stock price. This gives the put owner the right to sell the stock at a price higher than the market price, which in turn gives the option intrinsic value.
In this scenario, the put option’s underlying stock price is less than its strike price. Therefore, the option is trading in the money. Note that the option’s premium is irrelevant to determining the option’s intrinsic value; it would, however, be relevant to determining the option’s profit at exercise.
(Choice B) If the stock price equals the strike price, the option is trading at the money (ATM). At expiration, an ATM option is economically equivalent to owning the underlying asset.
(Choice C) For a call option, if the stock price is less than the strike price, the option is trading out of the money (OTM) and has no intrinsic value. The same is true for a put option if the stock price is greater than the strike price.
Things to remember:
Moneyness refers to the relationship between an option’s strike price and the underlying stock price. If the stock price equals the strike price, the option is trading at the money. For a call (put) option, if the stock price is greater (less) than the strike price, the option is trading in the money. For a call (put) option, if the stock price is less (greater) than the strike price, the option is trading out of the money.
An increase in which of the following is most likely to cause the value of both puts and calls to increase?
- Volatility
- Strike price
- Interest rate
Volatility refers to the dispersion of the underlying’s prices around its average price and is expressed as standard deviation (distance from the mean). More volatility means a wider range of prices for the underlying, so call and put options both have the potential for higher payoffs. This increased potential can cause time value to increase, which adds to the options’ overall value.
(Choice B) A call option’s strike (ie, exercise) price is inverse to the option’s premium (ie, price an investor pays for the option). Options with lower strike prices are more valuable than otherwise identical call options with higher strike prices since the intrinsic value for in-the-money call options is higher for lower strike options. The relationship between strike price and premium is positive for put options; a higher strike results in a higher premium for puts.
(Choice C) A high interest rate makes call options more valuable since the holder earns interest on the money that is not spent to purchase the underlying asset. By contrast, high interest rates reduce the present value of the expected payoff for a put option, so the put is worth less.
Things to remember:
Volatility of the underlying is a factor that affects the time value of options. Higher volatility increases the value of both put and call options. Higher strike prices increase the value of puts but reduce the value of calls. Higher discount (interest) rates increase the value of calls but reduce the value of puts.
Which of the following best replicates the cash flows of an interest rate swap? A series of:
- interest rate futures.
- interest rate call options.
- forward rate agreements.
Fixed-for-floating interest rate swaps are over-the-counter (OTC) derivatives in which counterparties agree to exchange a series of fixed payments for a series of floating payments. At each swap payment date:
- the floating payer owes cash to the fixed payer if the reference interest rate is greater than the swap’s fixed rate, or
- the fixed payer owes cash to the floating payer if the reference interest rate is less than the swap’s fixed rate.
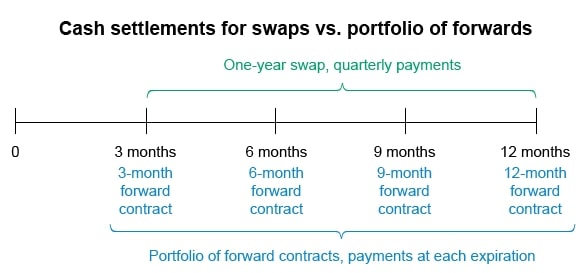
Swap cash flows are similar to forward rate agreements’ (FRAs’) cash flows (at expiration) since:
- the FRA seller (ie, short) pays the buyer (ie, long) if the reference interest rate is greater than the agreed rate, and
- the FRA buyer (ie, long) pays the seller (ie, short) if the reference rate is less than the agreed rate.
Given this similarity, the swap’s cash flows can be replicated by a portfolio of FRAs with expirations matching each swap payment date, all having agreed interest rates equal to the swap’s fixed rate.
(Choice A) Unlike FRAs, futures are exchange-traded derivatives that generate daily cash flows since they are marked to market every trading session. Although a portfolio of interest rate futures could create similar market exposure to that of an interest rate swap, a portfolio of futures could not replicate a swap’s cash flows.
(Choice B) Holders of interest rate calls never incur negative cash flows at expiration. Holders receive either the in-the-money call value in cash or nothing. In contrast, swaps may have positive or negative cash flows on the payment dates.
Things to remember:
A swap is equivalent to a portfolio of forward contracts. The portfolio consists of a forward contract for each swap payment date, each with an expiration coinciding with a swap payment date.
Copyright © UWorld. All rights reserved.
What to Expect in CFA Level 2 Derivative Investments
The CFA Level 2 Derivative Investments curriculum picks up where the Level 1 curriculum left off and further explores derivatives instruments and markets. It includes some of the curriculum’s more detailed and “mathy” portions as it dives into derivative pricing and valuation. It is often some of the least familiar material for applicants, making it more challenging to master.
Exam Weighting
The CFA Level 2 Derivative Investments topic has an exam weight of 5-10%, implying that around 4-8 questions or 1-2 item sets will focus on this topic.
| No. of Readings | No. of Formulas |
|---|---|
| 2 | Around 20 |
Level 2 Derivative Investments 2026 Syllabus, Readings, and Changes
The 2026 CFA Level 2 curriculum covers Derivative Investments across 2 learning modules. It’s important to highlight that there are no substantial changes in the Derivative Investments curriculum for CFA Level 2.
| No. of Readings – 2 | No. of LOS – 21 | |
|---|---|---|
Summary Introduces key pricing and valuation concepts of forward commitments, including forwards, futures, and swaps as well as valuation of contingent claims, that is, options. “Greeks,” which measure the effects on the value of small changes in underlying asset value, time, volatility, and the risk-free rate, are also discussed. | ||
Pricing and Valuation of Forward Commitments
The Pricing and Valuation of Forward Commitments learning module offers comprehensive insights into the pricing and valuation of forwards, futures, and swaps. It enhances your understanding by incorporating clear and easily digestible images and graphics.
The module covers the pricing and valuation of futures using various approaches, including the arbitrage-free method and offsetting bond portfolios. This content is particularly valuable for specialists relying on forwards and swaps to manage a wide array of market risks.
This knowledge is especially relevant for professionals such as private wealth managers, who employ futures to hedge their clients’ equity risk; pension scheme managers, who use swaps to mitigate interest rate risk; or university endowment managers, who utilize Derivative Investments for tactical asset allocation and portfolio rebalancing. The module can be customized to cater to the specific needs of these professionals.
Valuation of Contingent Claims
This reading centers on the binomial option valuation model, emphasizing the capacity to articulate and decipher its constituent elements. You will gain the ability to assess the worth of European options by factoring in the present value of anticipated payouts upon maturity. The material encompasses the identification of arbitrage opportunities, the computation of no-arbitrage values through a 2-period binomial model, and the interpretation of interest rate option values. It also delves into the assumptions and practical use of the Black-Scholes-Merton model in appraising a variety of options. Mastery of option Greeks, the execution of a delta hedge, the grasp of gamma risk, and the definition of implied volatility constitute the fundamental components of this succinct study.
CFA Derivative Investments Level 2 Sample Questions and Answers
These sample questions are typical of the L2 exam’s complexity and depth – formatted as item sets, with a vignette to deliver a scenario that tests the CFA L2 Curriculum. (On the actual exam, each vignette applies to 4 questions; we’ve provided a couple extra so you can practice thoroughly). Be sure to review the illustrated explanations we’ve provided for each question. UWorld’s question bank is designed to expose you to exam-like questions and explain the concepts tested thoroughly.
Based on Exhibit 1, the no-arbitrage 6-month forward price of Bond A is most likely:
- less than its spot price.
- equal to its spot price.
- greater than its spot price.
| Exhibit 1 5-Year German Government Bonds | |||
|---|---|---|---|
| Bond | Coupon rate | YTM | Price |
| Bond A | 0.00% | 3.00% | 86.261 |
| Bond B | 3.00% | 2.80% | 100.921 |
| Bond C | 5.00% | 2.85% | 109.889 |
No-arbitrage forward price
F0 = FV (S0 + CC0 – CB0 )
The no-arbitrage forward price of an asset is the:
- future value of the asset’s spot price, adjusted for the
- costs and benefits (ie, “carry” costs and benefits) of holding the asset to the forward contract expiration.
The forward price of a zero-coupon bond is just the future value of the bond’s spot price since there are:
- no explicit carry costs, due to the opportunity cost of capital being captured in the future value of the spot price, and
- no carry benefits since a bondholder receives no periodic coupon payments.
As a result, CC0 and CB0 in the formula above both equal 0, reducing the calculation of the no-arbitrage forward price to:
Zero-coupon bond forward contract price
F0 = FV ( S0 ) = S0 x (1 + r)T
r = Risk-free rate
T = Time to forward contract expiration
In this scenario, the 6-month forward price of the 5-year zero-coupon bond (ie, Bond A) is calculated as:
F0 = 86.261 (1.015)0.5 = 86.906
If interest rates are positive, the no-arbitrage forward price of an asset with no holding costs or benefits is greater than the asset’s spot price (Choices A and B). The spot/forward price difference reflects the opportunity cost of capital (eg, cost of financing a position in the asset) over the time to the forward contract expiration.
Things to remember:
The no-arbitrage forward price of an asset is the future value of the asset’s spot price adjusted for the costs and benefits of holding the asset to the forward expiration. The forward price of an asset with no holding costs or benefits is above the asset’s spot price by the opportunity cost of capital over the time to the forward expiration.
Based on Exhibit 1, the no-arbitrage 1-year forward price of Bond B is closest to:
- 99.880
- 99.939
- 102.939
| Exhibit 1 5-Year German Government Bonds | |||
|---|---|---|---|
| Bond | Coupon rate | YTM | Price |
| Bond A | 0.00% | 3.00% | 86.261 |
| Bond B | 3.00% | 2.80% | 100.921 |
| Bond C | 5.00% | 2.85% | 109.889 |
No-arbitrage forward price of coupon bond
F0 = FV (S0 + CC0 – CB0)
F0 = FV(S0 – CB0)
The no-arbitrage forward price of an asset is the future value of the asset’s spot price adjusted for the costs and benefits of holding the asset to the forward expiration. For a forward contract on a coupon bond, there are:
- carry benefits due to the coupon interest earned (plus reinvestment income on coupons received prior to expiration), and
- no explicit carry costs since the opportunity cost of capital is captured in the future value of the spot price.
Therefore, CC0 is dropped from the general forward pricing formula in the image above, so the no-arbitrage forward price calculation reduces to:
Coupon bond forward contract price
F0 = [ S0 – Cpn/(1 + r)T ] (1 + r)T
r = Opportunity cost of capital (eg, financing rate)
Cpn = Coupon amount
T = Time to forward contract expiration
In this scenario, the 1-year forward price of the 5-year 3% coupon bond (ie, Bond B) is calculated as follows:
F0 = [ 100.921 – 3.000/(1.02)1 ] x 1.021
(Choice A) 99.880 is the future value of the spot price minus the full coupon payment (ie, the future value of the coupon). The correct value is calculated by subtracting the present value of the coupon.
(Choice C) 102.939 is the future value of the spot price. This value does not capture the holding benefit of the coupon interest earned from owning the bond.
Things to remember:
There are no explicit carry costs in the forward pricing of securities since the opportunity cost of capital is captured in the future value of the spot price. Therefore, the no-arbitrage forward price of a coupon bond is the future value of the spot price minus the present value of interest earned (including reinvestment income on coupons received prior to expiration).
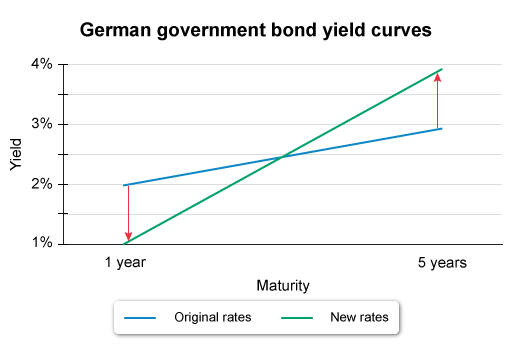
RZ goes long a 1-year forward contract on Bond C at the no-arbitrage forward price of 107.087. On the following day, the German government bond yield curve steepens, with the 1-year rate declining to 1.00% and Bond C’s YTM increasing to 3.85%. Based on its no-arbitrage value immediately after the yield curve shift, the value of RZ’s forward contract is most likely:
- negative.
- zero.
- positive.
No-arbitrage value of an existing forward contract
Vt = PV(Ft – F0)
= PV [ FV(St + CCt – CBt) – FV(S0 + CC0 – CB0)]
The value of an existing forward contract is the present value of the difference between the original forward price (F0) and the current no-arbitrage forward price (Ft) on an otherwise equivalent contract (ie, same underlying asset and expiration).
In this scenario, the primary factors affecting the forward contract’s value are the decrease of:
- the spot price due to an increase in Bond C’s YTM so that St < S0, and
- the opportunity cost of capital due to the lower 1-year interest rate, which results in a lower future value of the spot price to expiration.
Both factors reduce Ft relative to F0 (which was fixed at contract initiation), so RZ’s forward contract on Bond C has a negative value (Choices B and C).
Things to remember:
The value of an existing forward contract equals the present value of the difference between the original forward price and the current no-arbitrage forward price on an otherwise equivalent contract (ie, same underlying asset and expiration).
Copyright © UWorld. All rights reserved.
What to Expect in CFA Level 3 Derivative Investments?
Derivatives is not a stand-alone topic in Level 3, but derivatives concepts such as options, futures, swaps, and hedging techniques are embedded in portfolio construction, risk management, and currency management readings.
How to Study for CFA Derivative Investments?
Derivative Investments play a critical role in modern portfolio management, offering tools for hedging, risk management, and strategic exposure. To study this topic effectively, keep the following points in mind:
Derivative Investments’ Unique Role:
Derivatives differ from traditional assets because their value is derived from underlying instruments such as equities, fixed income securities, interest rates, or commodities. A strong conceptual understanding of how derivatives behave relative to their underlying assets is essential for mastering their use in risk management and portfolio construction.
Preparation Foundations:
Before diving into derivatives, ensure you have a solid grasp of core asset classes including equity, fixed income, and alternative investments as derivative pricing and payoff structures rely heavily on these fundamentals.
CFA Curriculum Focus by Level:
CFA Level 1 introduces the basic mechanics of forwards, futures, options, and swaps. Level 2 expands into derivative valuation, payoff diagrams, and position calculations. Level 3 emphasizes applying derivatives within portfolio management, including hedging, yield curve strategies, and risk adjustment techniques, often involving more complex numerical work.
Effective Study Strategies:
While memorizing key derivative formulas is important, focus on understanding the economic intuition behind each payoff and strategy. Consistent practice is critical work through CFA Institute end-of-chapter questions and use comprehensive QBanks and mock exams, such as those offered by UWorld, to build accuracy and speed.
Frequently Asked Questions (FAQs)
How can I study Level 2 Derivative Investments for the CFA exam?
The best way to study for the exam is to practice with a QBank across all chapters and readings. UWorld’s CFA Level 2 exam prep allows you to review your progress and acts as a catalyst for expediting your preparation. We also suggest you attempt practice problems from CFA Institute’s official Level 2 curriculum.
How do I practice CFA Level 2 Derivative questions?
CFA Level 2 Derivative Investments is considered a difficult and time-consuming topic. Working from practice problems given at the end of every reading in the CFA Institute’s official curriculum is not enough. Moving through a Qbank of other available resources is also helpful. After practicing, the best way to monitor your current understanding of the content is to take mock exams. UWorld’s CFA Level 2 test prep closely replicates the actual CFA Level 2 exam experience, keeping your foundations strong for the test day.
How do I practice CFA Level 2 Derivative formulas?
CFA Level 2 Derivative Investments is heavily sprinkled with complex calculations. That’s why complete knowledge and much more practice are the keys to success. Try to memorize formulas while doing practice problems, but also see them as mathematical representations of concepts.
How do I practice CFA L1 Derivative Investments questions?
After practicing hard with QBank, the optimal approach to assess your understanding of the content is taking mock exams. UWorld’s CFA mock exams closely replicate the actual CFA Level 1 exam to help you prepare and boost your confidence on test day. Like the actual CFA Exam, our mock exams consist of two 2-hour and 15-minute sessions (4.5 hours total), each with 90 multiple-choice questions unique to the mock exams. The question topics and the order of the topics follow the CFA exam design to give you a truly exam-like experience.
How do I practice the CFA L1 Derivative Investments formulas?
Understanding the concept first and then going through the structure of the formula will help you grasp the formula. Think of the formula as the mathematical representation of the concept. As you build this foundation of understanding, reinforce it through repetition and application. Look at our CFA L1 Formula sheet for further resources and tips.
What topics are included in the CFA Derivative Investments syllabus?
The Derivative Investments syllabus includes forwards, futures, options, swaps, credit derivatives, hedging strategies, option valuation models, binomial trees, Black-Scholes-Merton, Greeks, and strategies involving combinations of derivative positions, with Level 1 covering basic mechanics and Level 2 emphasizing valuation and payoff analysis.
How many Derivative Investments questions appear on the CFA exam?
Derivative Investments typically represents about 5–8% of the Level 1 exam, equaling roughly 9–14 questions, and around 5–10% of the Level 2 exam, corresponding to one to two item sets depending on the exam cycle.
What is the difference between Derivative Investments in Level 1 and Level 2?
Level 1 focuses on fundamental derivative concepts such as contract characteristics, payoff diagrams, and basic pricing relationships, while Level 2 goes deeper into valuation models, hedging applications, option Greeks, binomial valuation, and swaps pricing, requiring more quantitative work and interpretation.
Does Derivative Investments appear as a stand-alone topic in CFA Level 3?
Derivative Investments does not appear as a stand-alone topic at Level 3, but derivatives such as options, futures, and swaps are widely used within Portfolio Management for hedging, duration management, curve positioning, and risk control strategies.
Which Derivative Investments topics are considered the hardest?
The most challenging areas include option valuation using binomial trees and Black-Scholes-Merton, interpreting Greeks, swaps valuation, credit derivatives, and multi-step payoff and hedging strategies due to the combination of math and conceptual reasoning required.
Are derivatives heavily formula-based in the CFA exam?
Yes. Derivatives include many formulas involving payoffs, pricing relationships, forward rates, option valuation, swaps pricing, and risk sensitivities, making it one of the most formula-intensive CFA topics, especially at Level 2.
What formulas are most important in CFA Derivative Investments?
Key formulas include forward pricing formulas, option payoff formulas, Black-Scholes-Merton inputs, binomial valuation steps, effective interest rate adjustments, swap fixed-rate calculations, option parity relationships, and formulas for Delta, Theta, Gamma, Vega, and Rho. Visit our CFA Formula sheets page to download a free sample.